[인공지능] Entropy, CrossEntropy 이해

Information

정보이론에서 Information(정보량) 은 불확실한 상황을 결정하기 위해 필요한 정보량으로 정의되곤 합니다. 예를 들면 제가 1~100의 수 중 1가지 수를 선택했고 여러분이 수를 골라서 up / down 혹은 answer 이라는 대답을 받을 수 있으면 log100 번 물어보면 문제를 확실하게 맞출 수 있습니다.

 

어떤 사건이 발생할 확률이 p라면 p = (모든 상태수)의 역수 로 생각할 수 있으며, 정보량을 수식으로 나타내면

log(1 / p)

나타낼 수 있습니다. 이 때 log는 밑이 2인 log를 말합니다. 아래 예시를 통해 이해해보도록 하겠습니다. 

 

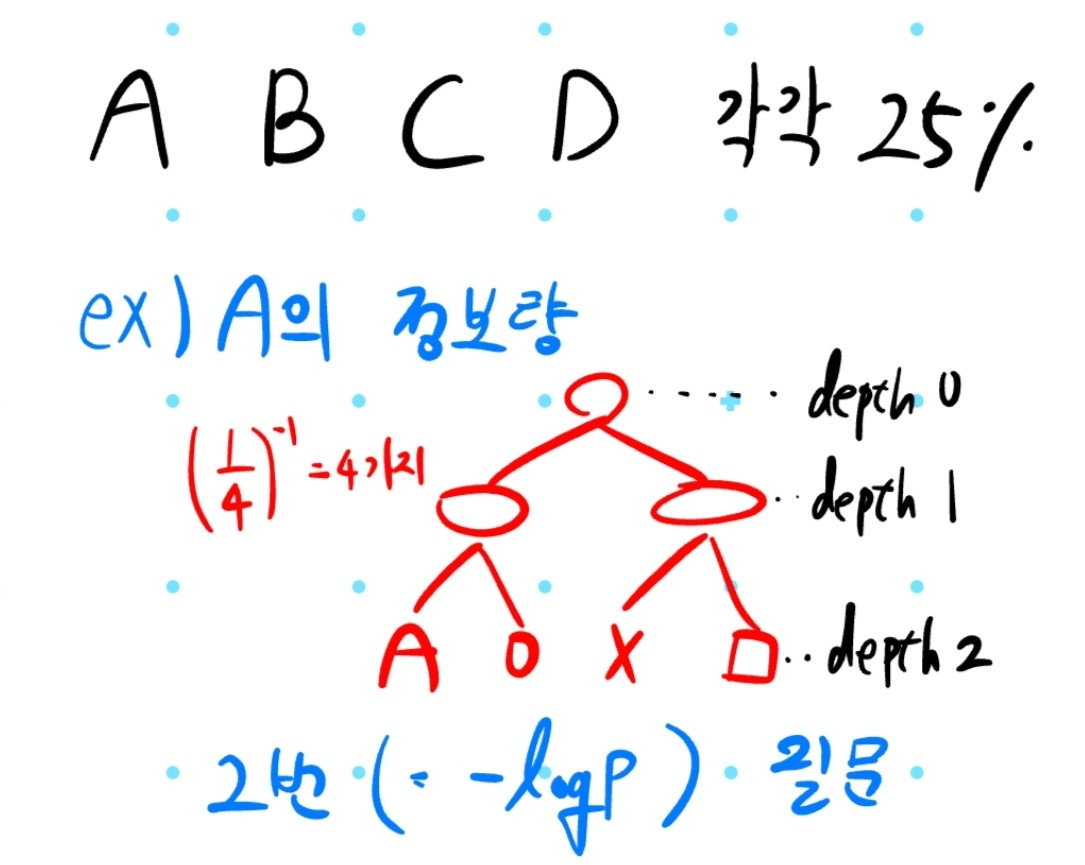
해당 예시에선 그림으로 나타내기 위해 2^k 꼴의 확률을 사용했는데 수학적으론 1/3이나 1/7... 등 상관 없습니다

 

 

Entropy

정보이론에서 Entropy는 확률분포 P(x)에서 정보량의 기댓값을 의미합니다. 정보량이 크다는 의미는 곧 불확실하다고 말할 수 있겠습니다. 따라서 식으로 나타내면

sigma( 확률 * 정보량 ) = sigma( p * log(1/p) )

 

로 나타낼 수 있습니다. 예시를 통해 이해해보죠!

 

 

CrossEntropy

CrossEntropy는 제가 생각하기에 2가지 정의가 존재한다고 생각합니다. 첫 번째는 확률 분포 P와 Q의 Entropy를 비교한다는 정의이고 제가 좋아하는 두 번째 정의는 실제값의 확률분포 P에 대하여 Q의 전략을 사용했을 때 정보량의 기댓값이라는 정의입니다. 

 

CrossEntropy는 "분류" 인공지능의 loss function으로 사용되는 친군데요. 인공지능에 접목하여 이해하기 위해서 2번째 정의가 더 좋다고 생각합니다. 이번엔 그림을 직접 드리진 않고 글을 읽고 상상해보죠! 

 

실제 데이터에선 A = 25%, B = 25%, C = 50% 인데 저희가 만든 model(전략)은 A=33%, B=57%, C=10%라고 하죠...

해당 전략을 실제 데이터에 적용할 때 Entropy를 계산한다면 A, B, C를 뽑을 확률은 실제 데이터와 같을 겁니다. 하지만 정보량은 model의 확률분포를 사용합니다. 

 

2번째 정의로 생각하면 이는 당연한 것처럼 느껴집니다. 실제 확률에다 저희가 설정한 model의 정보량의 곱, 이것을 식으로 나타내면

sigma( 실제 데이터 확률 * 전략의 정보량 ) = sigma(p log q)

꼴로 나타낼 수 있을 겁니다. 

 

 

"분류" 문제는 왜 MSE를 쓰면 안될까?

MSE말고 CrossEntropy function을 사용하는 까닭은 빠르고 안전하게 경사하강법으로 최적화하기 위해서 입니다. 일단 확률분포는 0~1로 정의되며 어떤 확률 분포 중에서 한 특징의 확률을 0.9라고 예측했는데 실제 값이 0.1이면 매~우 잘못 예측한거죠, 따라서 매우 큰 패널티를 부과해야 합니다. 

 

따라서 확률의 차의 제곱을 하는 것 보단 log함수를 이용한다면 큰 패널티를 부과할 수 있을 것이며 경사하강법에 의해 빠르게 학습될 것입니다. 

 

---

 

이번 포스팅에선 Entropy, CrossEntropy를 중심으로 분석해 봤는데요, 그냥 만들어진걸 딸깍 하고 쓰는 목적이라면 딱히 중요하진 않지만 loss function을 직접 디자인하고 연구를 하고 싶은 분들은 알아두는 것이 좋을 것 같습니다. 

 

최근에 인공지능 강연을 들으면서 loss function을 customize하여 어떤 상황에 얼마나 많은 패널티를 부과할지 이에 따라 어떤 함수를 사용할지 그런 내용을 인상깊게 들었는데요, CrossEntropy의 원리를 공부하고 이것을 사용하는 이유를 원리와 함께 이해하면서 다시 강연 내용을 더 깊게 이해할 수 있었던 것 같습니다.