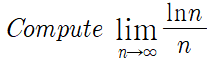가우스 소거법이나 역행렬 혹은 여러 factorization 을 사용하여 Ax = b의 해를 구하고자 노력했습니다. 하지만 일반적으로 해가 존재하지 않는 경우가 훨씬 많습니다. 이러한 경우에 orthogonal 개념을 이용하여 최소 오차를 구하고자 합니다! 1. 정사영 ( 배경 지식 ) 만약 b가 Col A 에 속하지 않다면 해는 존재하지 않습니다. 따라서 b는 아니지만 Col A에 속하는 원소 중, b와 거리가 가장 작은 값을 선택해야 합니다. 해당 포스팅에선 b hat 이라고 명명하겠습니다.  중학교에서 배웠듯이 가장 짧은 거리는 "직선" , "수직" 의 특성을 띈 수선입니다. 그렇다면 b hat은 어떻게 구할 수 있을까요? 해당 내용은 아래 글을 참고해주세요.  [전산수학I] Orthogonal의 ..

해당 개념을 소개하기 앞써 Orthogonal의 중요성은 언급하고자 합니다. Orthogonal은 직교를 뜻하며 일반적인 Basis 를 나중에 소개할 Gram-Schmidt 혹은 QR factorization을 활용해 직교 좌표계를 만든 후, 정사영 개념을 응용하여 "근사" 에 사용할 수 있습니다.  해당 개념이 너무 중요한 까닭은 일반적으로 방정식의 해를 구하지 못하는 경우가 대다수인데... 이럴 때 근사를 사용해서 가장 가까운 해와 그 오차에 대해서 구할 수 있기 때문입니다.  Inner Product(내적)  내적은 위의 식처럼 표현할 수 있으며 이를 기하적인 의미로 해석하기 위해 아래처럼 표기할 수 있습니다. 즉 v벡터의 크기와 t를 v에 정사영 했을 때의 길이의 곱이란 결과와 위의 결과들이 모두..

해당 포스팅에서 수열과 함수의 대응성과 단조수열정리에 대해 알아볼건데요, 시험에서 감점당하기 좋은.. 부분과 기초적인 부분을 중심으로 알아보겠습니다.  해당 포스팅은 Calculus Early Transcendentals 원서를 기반으로 작성했습니다. 이번 내용은 기초적인 내용이기에 짧습니다.. 1. 수열과 함수의 대응성 기본적으로 수열에서 로피탈은 사용할 수는 없습니다. 왜냐하면 수열은 실수에 대해서 정의된 것이 아닌 정수로 끊겨져 있기 때문입니다. 따라서 수열을 연속인 함수와 대응할 경우에만 로피탈을 사용할 수 있습니다. If lim x->infinity f(x) = L and f(n) = a_n (n = integer), then limit n->infinity a_n = Lf(n) = a_n 으로..

부분공간(Subspace)space, 공간은 벡터들의 집합을 말하는데, 어떤 공간 집합의 부분 집합을 Subspace라고 하며 아래 3가지 규칙을 만족해야 합니다. Let H is Subspace of Rn1. H는 zero vector를 포함해야 한다.2. H에 속하는 임의 벡터 u, v에 대하여 u+v 또한 H 집합에 속해야 한다.3. H에 속하는 임의 벡터 u에 대하여 cu 또한 H 집합에 속해야 한다. 이를 만족하는 Subspace도 크게 2가지로 나눌 수 있습니다. 1. Zero subspace - 오직 zero vector만 포함2. Nonzero subspace - 다른 vector들도 포함만약 Nonzero subspace라면 (2), (3)에 의해 무한한 크기의 집합이 될 것이며 선형적인..

1. 행렬끼리 곱(일반적) A = m by n, B = k by l 행렬, 즉 A = m행 n열, B = k행 l열 이라고 가정했을 때 행렬의 곱을 하기 위해서는 n = k여야 한다. 그 결과는 m by l 행렬, m행 l열로 나타나며 계산하는 방법은 A의 행과 B의 열을 차례대로 대응해서 곱하면 된다. 결과값은 아래와 같다. 2. 기하 관점 해석 위 그림은 아래와 같이 쓸 수 있다. 또한 Ax 꼴은 이전 포스팅에서 선형대수 Transformation 에서 서술했으므로 참고하면 된다. 물론 간단하게 이렇게 말해도 되지만 위의 설명을 모호하다. 따라서 더 자세하게 말하면 아래와 같다. 물론 작은 행렬을 계산할 때는 잘 알려진 방법으로 행렬의 곱을 계산하면 되지만 이를 물리나 데이터 분석에 사용할 때는 기하..

시험이 다가오고 있기에 성공적인 시험을 위해 감점받을 수 있는 요인 중 제가 했던 그리고 하고 있는 부분에서만 작성했습니다. 혹시 여러분들이 생각하는 다른 요인들이 있다면 댓글로 남겨주시면 감사하겠습니다. 아직 진도를 다 나간 것이 아니기에.. 짧지만 계속 추가하겠습니다. 1. Consistent 판단 [A b] 로 이루어진 경우 가장 오른쪽이 pivot position이라면 해당 행에서 A에 속한 원소들은 모두 0이며 b에 속한 원소만 값이 0 이 아니라는 뜻이 되기에 아래와 같이 서술할 수 있습니다. 이와 같은 경우 inconsistent, 즉 no solution이 됩니다. 2. Existence of Solution 처음 공부할 때 Existence of Solution이라는 말이 특정 해의 존재..

1. Limit Rule Limit Rule 말고도 정적분의 연산에서도 감점들이 자주 나오지만 위와 비슷하기 때문에 제외했다. 2. 미적분학 기본원리 1 3. 치환 적분 범위 설정 시험은 다가오고 있는데 문제를 풀 때마다 저도 아차! 하고 이거 감점당하겠네~ 하는 부분이 참 많았는데요. 그 중 가장 빈번히 발생하는 실수 요소들 3인방을 소개드렸습니다. 여러분도 시험볼 때 주의하고 맞왜틀? 내 점수 왜 이러지? 하지 마시고 좋은 성적 받길 바랍니다!

1. 용어 정의 2. 선형변환 이해 1) 설명 -> (x,y,z) 의 점으로 표현되고 상수일 수 있도, 아닐 수도 있지만, 계수의 관계성에 의해 임의 축과 다른 축의 값이 독립적이지 않을 수도 있음. 이 때 치역은 3차원 공간이지만 분포는 2차원... 인 꼴이다! 따라서 모든 b에 대해 해를 가지진 않음. ※ 이해 TIP Linear combination꼴로 해당 좌표계의 좌표축, 기저벡터로 값을 나타내는 과정으로 이해하는 것이 편함. 위에 처럼 이해할 시 값의 분포가 어떻게 이뤄지는지 생각하기 힘들지만 아래 처럼 이해하면 Range가 2차원인지 3차원인지 이해하기 쉬울 것 이다. 3. 선형연산과 좌표 1) 선형연산 2) 좌표축 ※ 선형 변환은 좌표축을 변환하는 것이라고 생각해볼 수 있다. (= 좌표계변..

1. Homogeneous System / Trivial Sol 1) Def 2) Exercise (feat. Parametric vector equation) 3) Exercise (feat. Nonhomogenous = general ) 2. Linear Independent 1) Def 3) Prove 4) Other Condition 3. 요약 1) Homogeneous ~ Ax = 0 인 Linear System을 뜻함. 이 때 x가 0이면 trivial, 아니면 intrivial 이라고 한다. Ax = b를 Parametric vector equation으로 나타내면 즉, free variable 에 대한 식으로 나타내면 결국의 b는 상수항과 비슷한 존재가 되기에 그냥 이항하면 $X_nho =..

1. arcsinh 2. arccosh 3. arctanh 4. arccsch 5. arcsech 6. arccoth 7. 정리 및 팁 삼각함수와 하이퍼볼함수의 역함수 미분을 외우기 쉬운 팁이 있다. 1) 도함수 사용 역함수의 도함수를 구하기 위해 f(y) = x꼴로 바꾼 후 미분하여 해당 식을 활용한다. 이를 통해 원래 함수의 도함수를 사용함을 알 수 있다. 2) 함수의 관계 이용 전개 과정에서 y를 x에 대한 식으로 전환하는 과정에서 원래 함수의 도함수와 관계있는 식을 이용해 y에 대한 함수를 x로 바꿀 수 있다. 이를 통해 대략적인 함수식을 떠올릴 수 있다. 3) 적용 sin과 cos의 경우 $sin^2x + cos^2x = 1$ 이라는 관계식을 통해 $1-x^2$을 연상할 수 있다. tan는 $t..