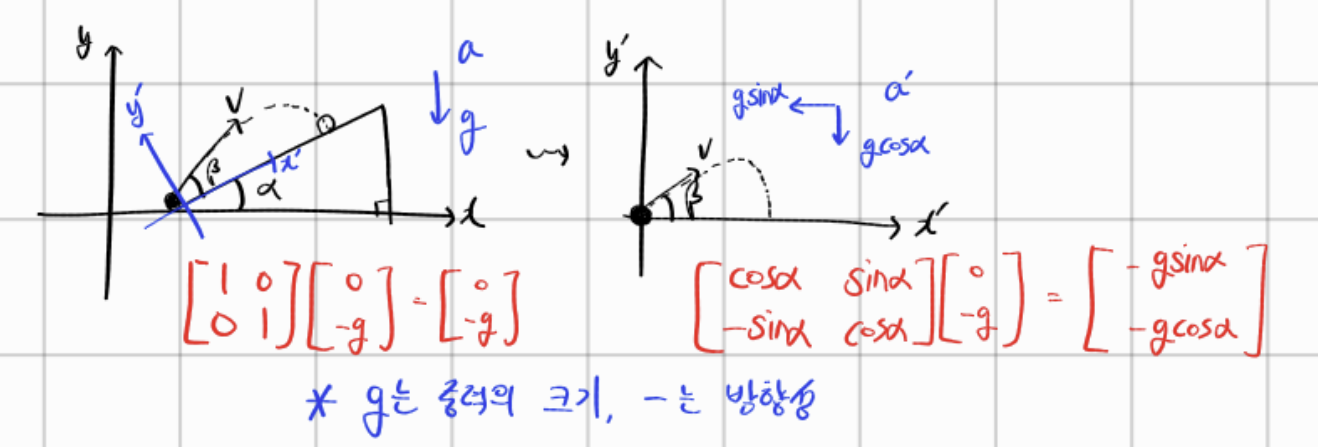
1. 행렬끼리 곱(일반적) A = m by n, B = k by l 행렬, 즉 A = m행 n열, B = k행 l열 이라고 가정했을 때 행렬의 곱을 하기 위해서는 n = k여야 한다. 그 결과는 m by l 행렬, m행 l열로 나타나며 계산하는 방법은 A의 행과 B의 열을 차례대로 대응해서 곱하면 된다. 결과값은 아래와 같다. 2. 기하 관점 해석 위 그림은 아래와 같이 쓸 수 있다. 또한 Ax 꼴은 이전 포스팅에서 선형대수 Transformation 에서 서술했으므로 참고하면 된다. 물론 간단하게 이렇게 말해도 되지만 위의 설명을 모호하다. 따라서 더 자세하게 말하면 아래와 같다. 물론 작은 행렬을 계산할 때는 잘 알려진 방법으로 행렬의 곱을 계산하면 되지만 이를 물리나 데이터 분석에 사용할 때는 기하..

시험이 다가오고 있기에 성공적인 시험을 위해 감점받을 수 있는 요인 중 제가 했던 그리고 하고 있는 부분에서만 작성했습니다. 혹시 여러분들이 생각하는 다른 요인들이 있다면 댓글로 남겨주시면 감사하겠습니다. 아직 진도를 다 나간 것이 아니기에.. 짧지만 계속 추가하겠습니다. 1. Consistent 판단 [A b] 로 이루어진 경우 가장 오른쪽이 pivot position이라면 해당 행에서 A에 속한 원소들은 모두 0이며 b에 속한 원소만 값이 0 이 아니라는 뜻이 되기에 아래와 같이 서술할 수 있습니다. 이와 같은 경우 inconsistent, 즉 no solution이 됩니다. 2. Existence of Solution 처음 공부할 때 Existence of Solution이라는 말이 특정 해의 존재..

1. Limit Rule Limit Rule 말고도 정적분의 연산에서도 감점들이 자주 나오지만 위와 비슷하기 때문에 제외했다. 2. 미적분학 기본원리 1 3. 치환 적분 범위 설정 시험은 다가오고 있는데 문제를 풀 때마다 저도 아차! 하고 이거 감점당하겠네~ 하는 부분이 참 많았는데요. 그 중 가장 빈번히 발생하는 실수 요소들 3인방을 소개드렸습니다. 여러분도 시험볼 때 주의하고 맞왜틀? 내 점수 왜 이러지? 하지 마시고 좋은 성적 받길 바랍니다!

1. 용어 정의 2. 선형변환 이해 1) 설명 -> (x,y,z) 의 점으로 표현되고 상수일 수 있도, 아닐 수도 있지만, 계수의 관계성에 의해 임의 축과 다른 축의 값이 독립적이지 않을 수도 있음. 이 때 치역은 3차원 공간이지만 분포는 2차원... 인 꼴이다! 따라서 모든 b에 대해 해를 가지진 않음. ※ 이해 TIP Linear combination꼴로 해당 좌표계의 좌표축, 기저벡터로 값을 나타내는 과정으로 이해하는 것이 편함. 위에 처럼 이해할 시 값의 분포가 어떻게 이뤄지는지 생각하기 힘들지만 아래 처럼 이해하면 Range가 2차원인지 3차원인지 이해하기 쉬울 것 이다. 3. 선형연산과 좌표 1) 선형연산 2) 좌표축 ※ 선형 변환은 좌표축을 변환하는 것이라고 생각해볼 수 있다. (= 좌표계변..

1. Homogeneous System / Trivial Sol 1) Def 2) Exercise (feat. Parametric vector equation) 3) Exercise (feat. Nonhomogenous = general ) 2. Linear Independent 1) Def 3) Prove 4) Other Condition 3. 요약 1) Homogeneous ~ Ax = 0 인 Linear System을 뜻함. 이 때 x가 0이면 trivial, 아니면 intrivial 이라고 한다. Ax = b를 Parametric vector equation으로 나타내면 즉, free variable 에 대한 식으로 나타내면 결국의 b는 상수항과 비슷한 존재가 되기에 그냥 이항하면 $X_nho =..