1. 행렬끼리 곱(일반적)
A = m by n, B = k by l 행렬, 즉 A = m행 n열, B = k행 l열 이라고 가정했을 때 행렬의 곱을 하기 위해서는 n = k여야 한다. 그 결과는 m by l 행렬, m행 l열로 나타나며 계산하는 방법은 A의 행과 B의 열을 차례대로 대응해서 곱하면 된다. 결과값은 아래와 같다.
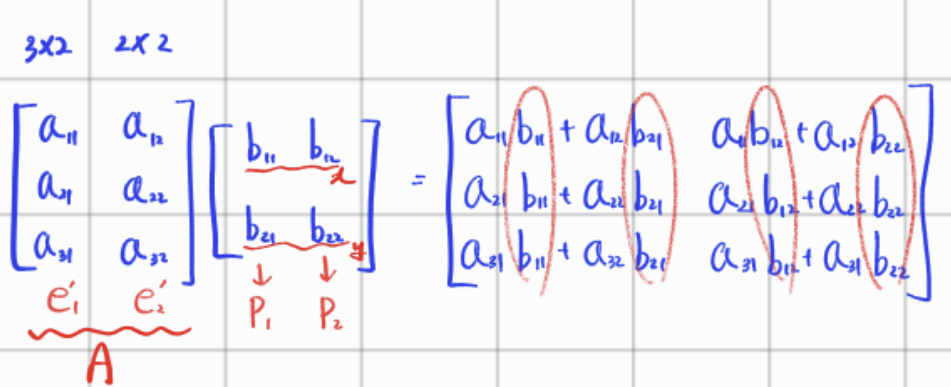
2. 기하 관점 해석
위 그림은 아래와 같이 쓸 수 있다. 또한 Ax 꼴은 이전 포스팅에서 선형대수 Transformation 에서 서술했으므로 참고하면 된다.

물론 간단하게 이렇게 말해도 되지만 위의 설명을 모호하다. 따라서 더 자세하게 말하면 아래와 같다.


물론 작은 행렬을 계산할 때는 잘 알려진 방법으로 행렬의 곱을 계산하면 되지만 이를 물리나 데이터 분석에 사용할 때는 기하적 의미를 알고 사용하는 것이 보다 해석하는데 도움된다.
3. 마무리
이번 포스팅은 매우 짧고 솔직히 구지? 싶은 부분이 있지만 그저 계산하기 위해서만 사용하는 것보단 의미를 알고 사용하는 것이 앞으로를 생각하면 더 도움이 되지 않을까? 해서 작성해봤다. 그리고 단순히 주어진 행렬의 곱을 구할 때는 이 내용이 딱히 필요없지만 우리가 행렬의 곱을 이용해서 상황을 해석해야 한다면 이 내용이 많은 도움이 될 것이다.
'대학 공부 > 전산수학I' 카테고리의 다른 글
| [전산수학I] Orthogonal의 기본적인 개념들 (0) | 2024.05.27 |
|---|---|
| [전산수학I] 부분 공간(Subspace)와 차원(Dimension/Rank) (0) | 2024.05.16 |
| [전산수학I] 풀이과정 팁 & 감점요인 (feat. Theorm) (0) | 2024.04.09 |
| [전산수학I] Linear Transformation(선형변환) (0) | 2024.04.06 |
| [전산수학I] Homogenous Linear System / Linear Independent (0) | 2024.04.04 |