1. 용어 정의

2. 선형변환 이해
1) 설명
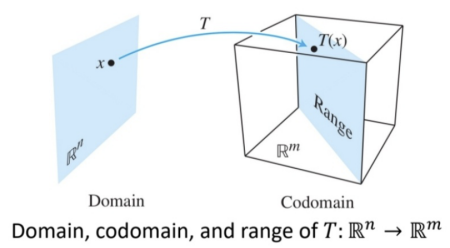

-> (x,y,z) 의 점으로 표현되고 상수일 수 있도, 아닐 수도 있지만, 계수의 관계성에 의해 임의 축과 다른 축의 값이 독립적이지 않을 수도 있음. 이 때 치역은 3차원 공간이지만 분포는 2차원... 인 꼴이다! 따라서 모든 b에 대해 해를 가지진 않음.
※ 이해 TIP

Linear combination꼴로 해당 좌표계의 좌표축, 기저벡터로 값을 나타내는 과정으로 이해하는 것이 편함. 위에 처럼 이해할 시 값의 분포가 어떻게 이뤄지는지 생각하기 힘들지만 아래 처럼 이해하면 Range가 2차원인지 3차원인지 이해하기 쉬울 것 이다.
3. 선형연산과 좌표
1) 선형연산

2) 좌표축

※ 선형 변환은 좌표축을 변환하는 것이라고 생각해볼 수 있다. (= 좌표계변환)
4. Onto / One to one
1) Onto

왼쪽 그림의 경우 m차원을 최대한 활용하지 못하여 분포가 m차원 미만으로 나타날 경우, 오른쪽은 m차원을 다 활용하여 치역자체가 m차원의 Span일 경우를 의미함. (치역 = 공역)
2) One to One
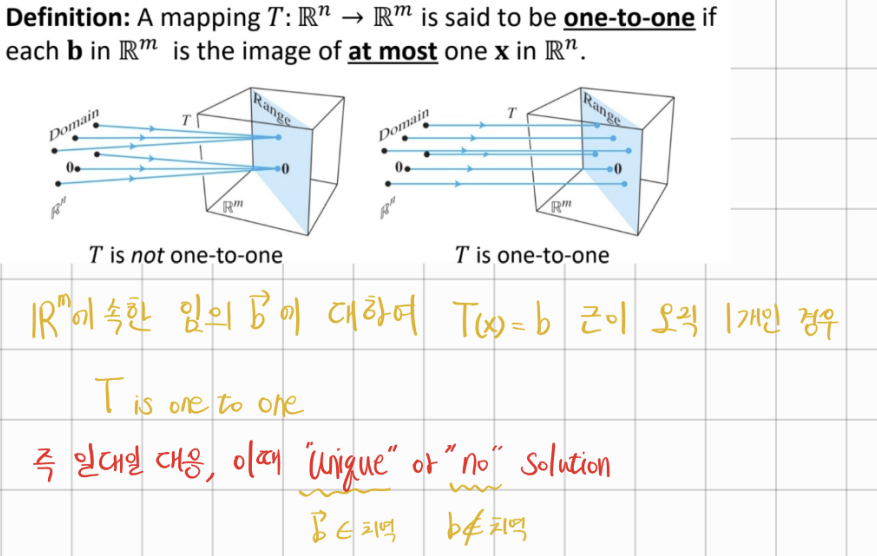
왼쪽 그림의 경우 치역의 값을 표현하는 방법이 여러 가지임을 나타내며 오른쪽은 표현하는 방법이 1가지 이지만 공역일 경우는 표현하지 못함을 의미함. ( One to One은 Existence가 아닌 Uniqueness 를 따지는 것이기 때문이다.
3) 차원적 해석

3차원은 수 많은 2차원으로 이루어짐... 하지만 2차원은 3차원의 극 일부에 불구함.. 이 사실을 Onto, One-to-One 에 적용하면 이해하기 편함.
4) 판별법

Row에 pivot이 없는 경우가 없다면 해당 차원의 값을 표현할 수 없음 -> 표현의 차원성 ↓
Colum에 pivot이 없는 경우 Free variable 존재함.
※ 가끔 하는 실수

'대학 공부 > 전산수학I' 카테고리의 다른 글
| [전산수학I] 행렬과 행렬의 곱셈 (feat. 기하적 해석) (0) | 2024.04.11 |
|---|---|
| [전산수학I] 풀이과정 팁 & 감점요인 (feat. Theorm) (0) | 2024.04.09 |
| [전산수학I] Homogenous Linear System / Linear Independent (0) | 2024.04.04 |
| [전산수학I] Vector, Matric, and Solution Set (feat. 종합정리) (0) | 2024.03.27 |
| [전산수학I] Solving Systems of Linear Equation (0) | 2024.03.26 |