해당 개념을 소개하기 앞써 Orthogonal의 중요성은 언급하고자 합니다. Orthogonal은 직교를 뜻하며 일반적인 Basis 를 나중에 소개할 Gram-Schmidt 혹은 QR factorization을 활용해 직교 좌표계를 만든 후, 정사영 개념을 응용하여 "근사" 에 사용할 수 있습니다.
해당 개념이 너무 중요한 까닭은 일반적으로 방정식의 해를 구하지 못하는 경우가 대다수인데... 이럴 때 근사를 사용해서 가장 가까운 해와 그 오차에 대해서 구할 수 있기 때문입니다.
Inner Product(내적)

내적은 위의 식처럼 표현할 수 있으며 이를 기하적인 의미로 해석하기 위해 아래처럼 표기할 수 있습니다.


즉 v벡터의 크기와 t를 v에 정사영 했을 때의 길이의 곱이란 결과와 위의 결과들이 모두 같습니다.
Orothogonal 이란?
Orothogonal 은 "수직인, 직교하는" 의 의미를 가지며 두 벡터의 내적값이 0임을 뜻합니다. 만약 이를 만족한다면 당연하게 피타고라스 법칙이 성립합니다.
Orothogonal Set / Basis

Orthogonal Set의 정의는 위와 같습니다. 이 때 주의할 점은 해당 벡터들이 모두 선형독립이 아닐 수 있다는 사실입니다. Orothogonal 의 의미는 "직교하는"의 뜻을 가지기 때문에 해당 집합에 존재하는 임의 두 벡터의 내적이 0이면 모두 직교하므로 선형 독립일 것 같지만, 한 가지 사실을 간과하고 있는게 있습니다. 그것은 바로 0 벡터의 존재성입니다.

따라서 Nonzero Vector임을 추가적으로 명시해주면 해당 벡터들은 모두 선형 독립이 되며 Basis로 기능하게 됩니다.
Orothonormal
Orothogonal, Normalizing 두 개념을 합친 내용입니다. 즉 해당 집합의 임의 두 벡터의 내적값은 0이며 모든 벡터의 크기가 각각 1입니다. 벡터의 크기가 1이기에 모두 nonzero vector임이 보장됩니다.
Orthogonal Projection

벡터 y, v 가 주어졌을 때 "orthogonal projection of y onto u" 즉 y를 u로 정사영한 벡터를 구하고 싶습니다. 내적의 기하적인 의미를 생각하면 내적값 yv = αv * v 임을 알 수 있으며 α = (y*v) / (v*v) 라는 사실을 어렵지 않게 얻을 수 있었습니다.

이 때 y위에 ^이 달린 것을 정사영 벡터라고 하며 proj_v (y) 라고 표기하곤 합니다. 따라서 v벡터와 수직인 벡터는 y - proj_v(y) 로 구할 수 있습니다.

위 내용을 확장하면 고차원에 대해서 같은 원리로 서술할 수 있으며 식으로는 아래처럼 나타낼 수 있습니다.
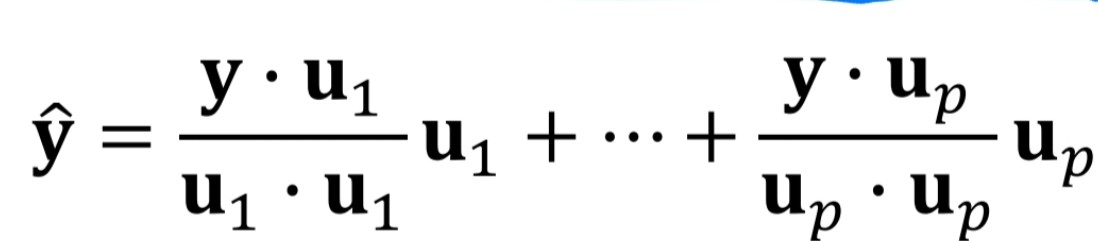
해당 개념에서 주의할 점은 분모에 u_1 이 존재하므로 약분하면... 각각의 cu 값들이 y고 이것이 p개 있는 것 아닌가? 라고 생각하실 수도 있는데 절~대 아닙니다. 일단 왼쪽 값은 scalar 이며 이를 벡터로 다시 쪼갠 후 연산할 수도 없으며 벡터*벡터, 벡터*스칼라가 다른 곱이라서 그렇게 생각하시면 안됩니다... 해당 개념은 정사영의 개념으로 사고하시면 됩니다.
더 나아가 만약 Orthonormal Set 이었다면 분모의 값은 모두 1이 되고 결국 y와 u_i 의 내적값을 가중치로 갖는 선형 결합임을 알 수 있습니다. 따라서 이를 더~ 간단하게 나타내 보자면
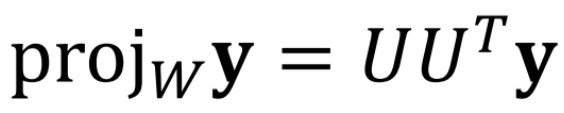
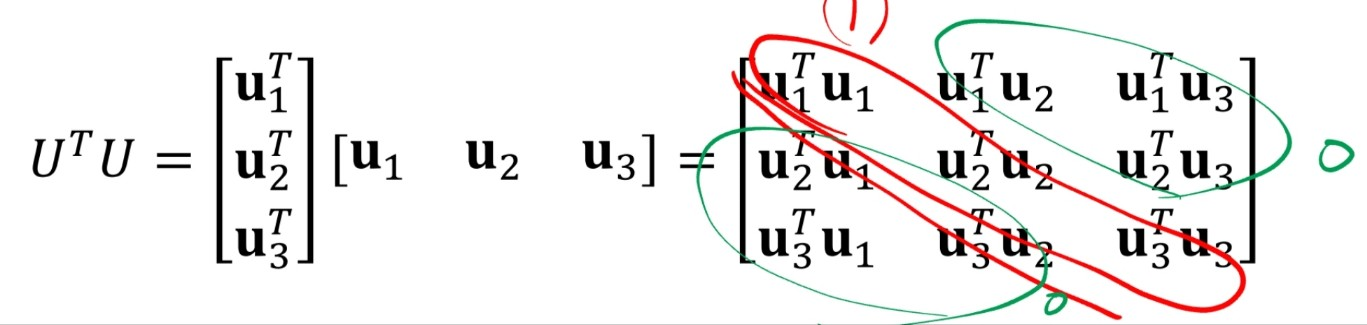
위 두 가지의 성질을 가지게 됩니다. (두 식이 의미하는 바는 다릅니다). 첫 번째 식은 위에서 orthogonal projection 을 더 간단하게 일반화한 방법인데요, 해당 식은 U ( U^T y ) 로 곱하는 순서? 우선 순위를 바꿨다고 생각하면 각 벡터들과 y의 내적값의 가중치를 갖는 벡터들의 선형조합이라고 이해할 수 있습니다.
이 때 곱하는 순서라는 것은 AB => BA 라는 뜻이 아닙니다.
오늘은 Orothogonal 의 기본적인 개념과 햇갈리는 개념들을 소개해봤습니다. 주의할 점은 Orothogonal Set과 Basis의 차이점에 대해 알아봤고 벡터 묶음들을 행렬을 이용해 내적하는 방법, 정사영에 대해 알아봤습니다.
정사영이 중요한 이유는 일반적으로 Ax = b 를 구할 때 해를 구할 수 없는 경우가 많습니다. 그럴 때 오늘 소개한 개념을 활용해서 최소 오차가 되도록 근사할 수 있습니다. 다음 포스팅에선 근사와 직교 좌표계를 구하는 방법에 대해 소개하겠습니다.
참고) Orthogonal Matrix는 Square Matrix + orthogonal of nonzero
'대학 공부 > 전산수학I' 카테고리의 다른 글
| [전산수학I] Least-Squre-Method 최소 오차 (feat. 선형변환) (0) | 2024.06.24 |
|---|---|
| [전산수학I] 부분 공간(Subspace)와 차원(Dimension/Rank) (0) | 2024.05.16 |
| [전산수학I] 행렬과 행렬의 곱셈 (feat. 기하적 해석) (0) | 2024.04.11 |
| [전산수학I] 풀이과정 팁 & 감점요인 (feat. Theorm) (0) | 2024.04.09 |
| [전산수학I] Linear Transformation(선형변환) (0) | 2024.04.06 |