참고 블로그 : https://blog.naver.com/kks227/220804885235
저는 kks227(라이) 님의 블로그를 자주 보는데요. 이번에 최대 유량 알고리즘을 공부할 때도 이 분의 블로그를 메인으로 보고 다른 문서들이랑 같이 봤습니다. 혹시.. 문제가 된다면 내리겠습니다.
개인적으로 이분탐색을 먼저 공부했기에 많이 햇갈렸는데요, 그래서 다른 분들도 최대한 이해하기 쉽게 설명할라고 합니닷..
1. Main Idea
1) 용어 설명
- 용량 : c(u, v) - 정점 u->v로 전송할 수 있는 최대 용량
- 유량 : f(u,v) - 정점 u->v로 흐르고 있는 유량
- 잔여 용량 : r(u,v) - 정점 u->v로 더 흐를 수 있는 유량
- 소스 : 시작점
- 싱크 : 도착점
2) 규칙
1. 용량 제한 : f(u,v) <= c(u,v)
2. 유량의 대칭성 : f(u,v) = -f(v,u)
3. 유량의 보존성 : 들어오는 유량 = 나가는 유량
다른 규칙은 몰라도 "유량의 대칭성" 은 이 알고리즘의 핵심입니다!!
2. 포드 풀커슨 / 에드몬드-카프 알고리즘
네트워크 플로우는 매우 많은 알고리즘이 존재하며 각 알고리즘 마다 시간복잡도나 구현 난이도 등 다양합니다. 하지만 가장 기본적이고 보편적인 알고리즘 2개에 대해 설명하고자 합니다.
| 포드 풀커슨 | 에드몬드 카프 | |
| 탐색 방법 | dfs | bfs |
일단 두 알고리즘은 같은 아이디어로 작동하며 차이는 탐색 방법만 다릅니다. 아래 예시를 통해 설명하겠습니다.

컴퓨터가 그래프를 탐색할 때 입력에 따라 탐색하는 순서가 다르다.
사람은 가끔 이상적인 상황을 생각하지만 입력값이 운이 안좋아 오류를 일으키곤 합니다. 따라서 이를 고려하여 알고리즘을 구현해야 합니다.
| dfs | bfs |
 |
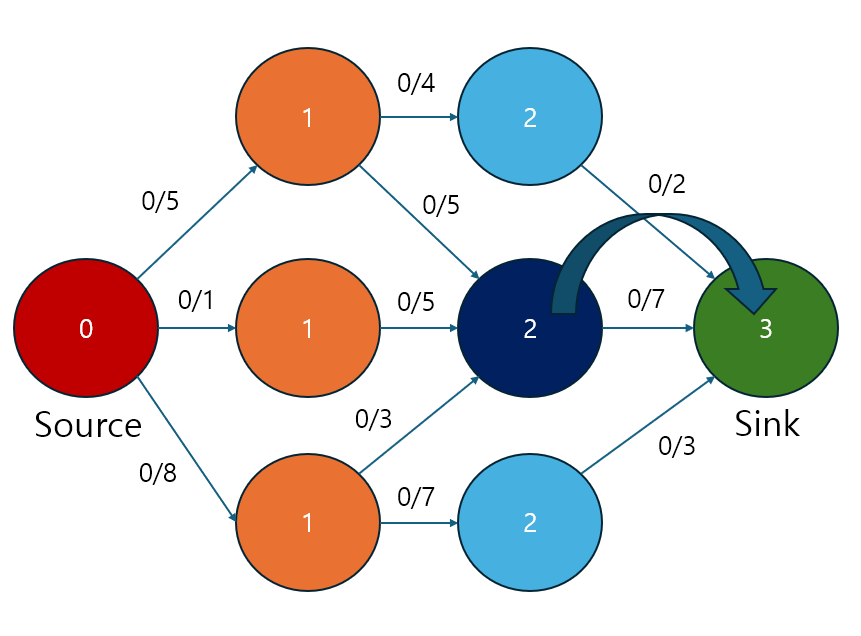 |
dfs와 bfs모두 Source에서 Sink로 가는 경로를 탐색합니다. dfs는 당연하지만 bfs는 햇갈릴 수도 있는게, 결국 1개의 경로에 대해서만 작업을 한다는 것 입니다. 그렇다면 왜 bfs를 사용해야 할까? 라는 의문이 생기지만 그것은 뒤에서 다뤄보겠습니다.
위의 예시 그림에서는 dfs/bfs가 모두 같은 경로를 찾은 모습입니다. 그렇다면 이 한가지 경로를 Sink에서 시작하여 trace해주고 그 과정에서 잔여 용량의 최솟값을 구합니다. 이는 해당 경로에서 흐를 수 있는 최대 유량이라고 말할 수 있습니다.

해당 경로에서 흐를 수 있는 최대 량은 5이므로 위 처럼 표현할 수 있습니다. 여기서 중요하게 볼 것은 -5/0 의 역방향 경로가 생겼다는 사실입니다. 이것은 유량의 대칭성을 나타내는 것이며 "음의 유량" 이라고 생각하기 보다는 "반대로 흐를 수 있는 능력" 이라고 생각하시는 것이 좋을 것 같습니다.
쫌더 진행해 보자면(dfs로 진행중)
사실 음의 간선 다 표기해야 하지만 중요한 음의 간선만 표기했습니다...

해당 경로에서 잔여 유량의 최솟값은 1임을 알 수 있습니다. 따라서 갱신해주고... (물론 다른 경로에 대해서도 역간선을 추가해야 하지만 그 부분은 해당 예시를 푸는데 중요하지 않기 때문에 그리지 않았습니다.)

그리고 다른 경로를 탐색해보다 위와 같은 경로가 나타났고 또 갱신해줍니다....

그리고 또 탐색해보니 대충 볼 때는 거의 다 완성 된것 같네요.
따라서 정답은 10입니다! 라고 말해도 되는 걸까요?? 당연히 안됩니다. 그 까닭은 아직 증가 경로를 더 만들 수 있기 때문입니다. 대충 보기에는 더 이상 흐를 수 있는 통로가 없어보이지만 음의 간선이 f < c 를 만족하기에 아직 더 흐를 수 있는 통로가 있다고 생각할 수 있습니다. ( -5/0 은 역방향으로 0/5 로 볼 수 있습니다. 따라서 아직 더 흐를 수 있습니다.)
 |
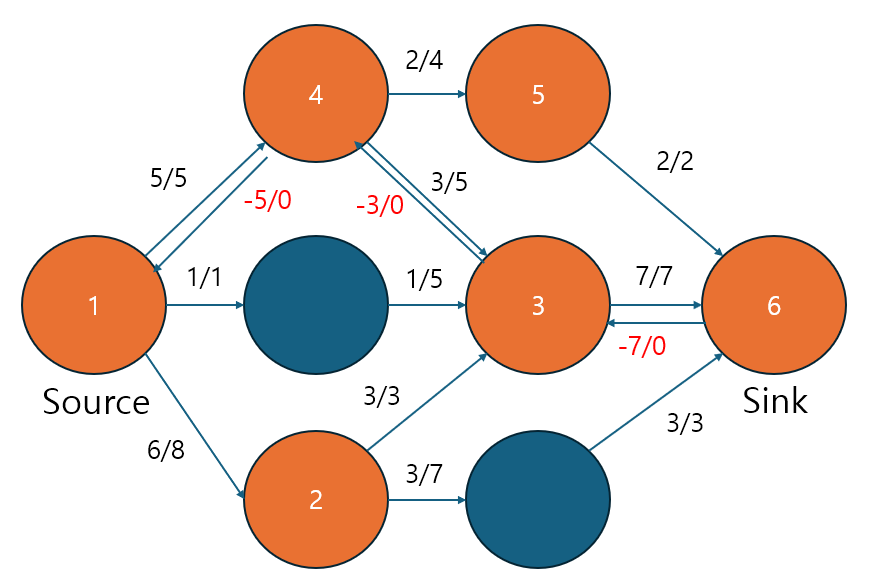 |
위와 같은 경로를 찾았다고 할 때 잔여 용량, 즉 c-f 는 min(8-4, 3-1, 0-(-5), 4-0, 2-0) = 2입니다. 따라서 이를 고려하여 나타낸다면 오른쪽과 같이 나타낼 수 있습니다. 그렇다면 정답은 12라고 말할 수 있겠네요! (왼쪽은 경로 찾고, 오른쪽은 갱신한 모습)
유량이 -a (a는 양수) 다 라는 것은 반대 방향으로 최대 유량이 a다 라는 것 입니다. 이는 역방향으로 흐를 수 있는 능력이 존재한다는 의미라고 볼 수 있습니다.
3. dfs를 쓰지 않는 이유
그렇다면 왜 dfs를 쓰지 않을까요? dfs나 bfs나 별 다를 것 없어보이는데...
이상적인 상황이라면 dfs/bfs상관 없지만 입력에 따라 싸이클(?) 같은게 발생하기 때문입니다.

매우 유명한 예시인데요, 입력이 운이 안좋게도 1->2->3->4->5 / 1->4->3->2->5 로만 작동하게 된다면... 최대 유량은 1인 경로가 되는데... 9999 * 2 번 탐색 해야하게 됩니다...
이상적으로 생각할 땐 그냥 1->2->5 나 1->4->5 로 가면 되는데.. 왜.. 라고 생각할텐데요. 컴퓨터는 그런거 모릅니다. dfs로 구현할 경우 이런 이상한 상황이 발생하기에 O(Ef) 의 시간복잡도를 가질 수 있다고 합니다 (f는 최대 유량입니다)
그렇다면 bfs는 어떨까요? bfs는 최소 간선 + 최대 유량이기에 저런 이상한 경우는 무시하고 1->2->5 라는 경로를 탐색할 수 있습니다.
4. 햇갈리는 부분
bfs는 한 가지 경로를 탐색하고 해당 경로의 잔여 유량의 최솟값으로 유량이 흐른다고 계산하기 때문에 위와 같은 문제가 발생한다고 생각하였습니다. 그리고 bfs의 경우 그나마 인접 노드에 대해서만 계산하기에 괜찮을 거라고 생각했는데... 이는 잘못된 것입니다.
bfs또한 dfs와 마찬가지로 1가지 경로를 찾습니다. 이 때 다른점은 bfs는 "최단 간선의 경로를 찾는다" 라는 부분에서 위와 같은 문제가 생기지 않음을 알 수 있습니다. 그 후에 Sink에 도착한다면 마찬가지로 trace하여 최소 잔여 유량찾고 갱신해줍니다.
5. 연습 문제 및 코드
https://www.acmicpc.net/problem/6086
백준 6086번 최대 유량문제 입니다. 제목도 그렇고.. 대놓고 최대 유량 알고리즘이다! 라고 말하고 있는데요. 일단은 최대 유량 알고리즘의 가장 기본적인 문제로 써 코드를 짜봤습니다.
#include <bits/stdc++.h>
using namespace std;
#define E 25
#define S 0
#define INF 21e8
int N, c[60][60], f[60][60], ans;
vector<int> near[60];
int c2n(char str)
{
if('A'<=str&& str <= 'Z')
return str - 'A';
return str - 'a' + 26;
}
int main()
{
char c1, c2;
int cost;
ios_base::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
cin >> N;
for(int i=0;i<N;i++){
cin >> c1 >> c2 >> cost;
int n1 = c2n(c1), n2 = c2n(c2);
c[n1][n2] += cost, c[n2][n1] += cost;
near[n1].push_back(n2); near[n2].push_back(n1);
}
int trace[60], arrive, chk[60];
while(1){
memset(trace, -1, sizeof(trace));
memset(chk, 0, sizeof(chk));
arrive = S;
queue<int> q;
q.push(0);
while(!q.empty() && arrive!=E){
int loc = q.front();
q.pop();
for(auto&i:near[loc]){
if(c[loc][i] - f[loc][i] > 0 && !chk[i]){
q.push(i);
trace[i] = loc, arrive = i, chk[i] = 1;
if(arrive == E) break;
}
}
}
if(arrive != E) break;
int min_value = INF;
for(int i = arrive; i!=S; i=trace[i]) min_value = min(min_value, c[trace[i]][i] - f[trace[i]][i]);
for(int i = arrive; i!= S; i=trace[i]){
f[trace[i]][i] += min_value;
f[i][trace[i]] -= min_value;
}
ans += min_value;
}
cout << ans;
}
해당 문제에서는 문제가 되지 않았지만... 단방향 간선일 때는... c[y][x]처럼 역방향 c를 초기에 설정할 필요는 없지만 인접벡터 (연결 상태를 나타내는 벡터) 는 역방향 간선도 추가는 해둬야 합니다!!!
제 인생에서 대학의 첫 시험을 경험하고 맨탈이 굉장히 털렸는데요... 그냥 저는 학점에 크게 연연하지 않고 하고 싶은 공부나 하려고 합니닷.. 그래서 이번에 네트워크 유량 알고리즘에 대해서 공부해 봤는데요, 만약 틀린 부분이 있다면 지적해주세요! ( 언제나 환영입니다! )
위의 예시는 ppt로 제가 만든거다 보니.. 퀄리티도 떨어지고... 약간 틀릴 수도 있습니다. 시험이 끝나서 그런지 쫌 참아왔던 걸 이렇게 하니깐 기부니가 좋네용 ㅎㅎ
틀린 부분, 오개념, 애매한 부분, 질문 등 모두 환영합니다!
'코딩 > 알고리즘' 카테고리의 다른 글
| [알고리즘] 강한 연결 알고리즘 SCC (feat. 2150번) (0) | 2024.05.09 |
|---|---|
| [알고리즘 문제] 2316번 도시 왕복하기 2 (1) | 2024.05.01 |
| [알고리즘 문제] 13250번 주사위 게임 (feat. 탑-다운, 바텀-업) (0) | 2024.04.12 |
| [알고리즘 문제] 1521번 랜덤 소트 (0) | 2024.04.10 |
| [알고리즘 문제] 27730번 견우와 직녀 (0) | 2024.04.08 |