[미적분학] 역쌍곡선 함수의 미분 - feat. 역삼각함수

1. arcsinh

 

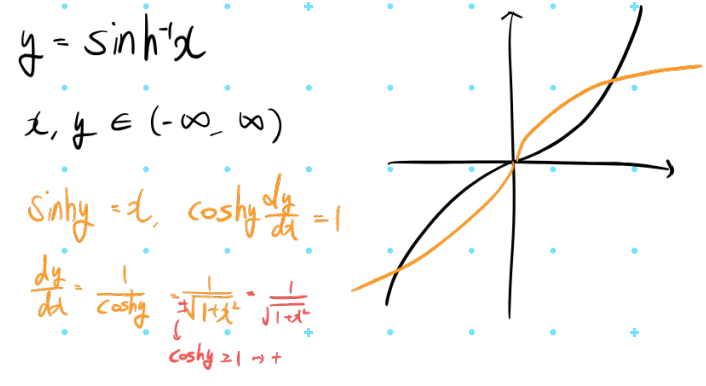
2. arccosh

 

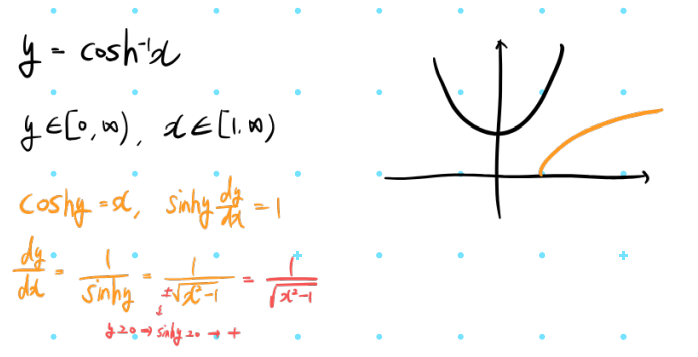
3. arctanh

 

 

4. arccsch

 

 

5. arcsech

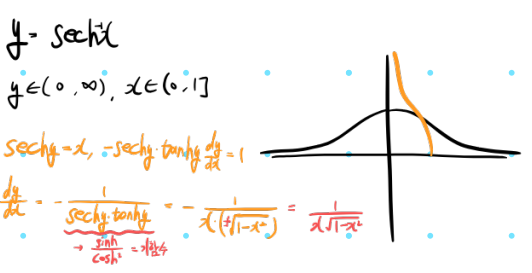
6. arccoth

 

7. 정리 및 팁

출처 https://blog.naver.com/PostView.nhn?blogId=ldj1725&logNo=80177012304

삼각함수와 하이퍼볼함수의 역함수 미분을 외우기 쉬운 팁이 있다.

 

1) 도함수 사용

역함수의 도함수를 구하기 위해 f(y) = x꼴로 바꾼 후 미분하여 해당 식을 활용한다. 이를 통해 원래 함수의 도함수를 사용함을 알 수 있다.

 

2) 함수의 관계 이용

전개 과정에서 y를 x에 대한 식으로 전환하는 과정에서 원래 함수의 도함수와 관계있는 식을 이용해 y에 대한 함수를 x로 바꿀 수 있다. 이를 통해 대략적인 함수식을 떠올릴 수 있다.

 

3) 적용

sin과 cos의 경우 $sin^2x + cos^2x = 1$ 이라는 관계식을 통해 $1-x^2$을 연상할 수 있다. tan는 $tan^2x + 1 = sec^2x$ 라는 관계로 $1+x^2$식을 떠올릴 수 있다. 또한 sec, csc함수의 미분형은 sectan , -csccot 꼴이며 sec, csc를 통해 tan, cot을 유도할 수 있다. 마찬가지로 역쌍곡선함수에도 $cosh^2x - sinh^2x = 1$ 이라는 관계식과 원래 함수의 도함수의 형태를 통해 알 수 있다.

 

함수의 부호나 절댓값의 여부는 원래 함수의 도함수가 치역(y)에서 +인지 -인지를 확인하여 구할 수 있다. 

 

 

해당 사실을 통해 역삼각함수, 역쌍곡선함수의 미분을 암기해야 한다.. 그리고 적분 문제에 활용되는 경우는 sin, cos, tan, sinh, cosh, tanh, coth 가 가장 잘 나오는 것 같다. 그리고 문제를 보고 어떻게든 위와 같은 형태로 이끌어가는 연습이 많~이 필요할 것 같다... 시험이 1달도 안남았다니..