해당 포스팅에서 수열과 함수의 대응성과 단조수열정리에 대해 알아볼건데요, 시험에서 감점당하기 좋은.. 부분과 기초적인 부분을 중심으로 알아보겠습니다. 해당 포스팅은 Calculus Early Transcendentals 원서를 기반으로 작성했습니다. 이번 내용은 기초적인 내용이기에 짧습니다..
1. 수열과 함수의 대응성
기본적으로 수열에서 로피탈은 사용할 수는 없습니다. 왜냐하면 수열은 실수에 대해서 정의된 것이 아닌 정수로 끊겨져 있기 때문입니다. 따라서 수열을 연속인 함수와 대응할 경우에만 로피탈을 사용할 수 있습니다.
If lim x->infinity f(x) = L and f(n) = a_n (n = integer), then limit n->infinity a_n = L
f(n) = a_n 으로 대응되는 어떤 함수 f(x)에 대하여 f(x) 극한값이 L이면 a_n 의 극한값도 L이다.
예시 문제 1)
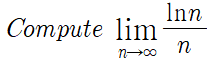
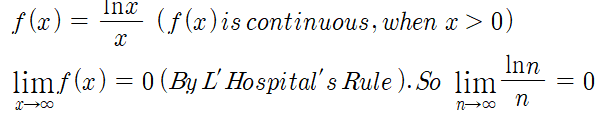
주의할 문제


일단 이 문제는 로피탈을 쓰고 싶지는 않지만 애초에 쓸 수 없습니다. 왜냐하면 factorial 함수는 음이 아닌 정수에서 정의되었기에 f(x) 로 대응시킬 수 없기 때문입니다. 원서의 해설은 아래와 같습니다. 따라서 수열의 극한을 계산할 때 대부분 그냥 함수의 극한값을 계산하는 것 처럼 계산하실 수 있는데, 함수로 대응시킬 수 있음을, 즉 n에서 연속함을 보여야 합니다. (교바교로 감점할 수도..)
단조수열 정리
Every bounded, monotonic sequence is convergent.
유계한 단조수열은 수렴한다.
단조수열은 오직 증가 or 감소만 하는 수열을 의미합니다. 따라서 단조 증가 수열 / 단조 감소 수열 2가지로 나뉩니다. 그리고 유계한(bounded) 는 상한과 하한이 존재한다는 의미입니다. 상한은 수열의 천장을 의미하며 하한은 바닥을 의미합니다. 상한과 하한은 Unique하지 않지만 Least Upper bound (최소 상한) 같은 것은 Unique합니다.
이렇게 풀어서 설명하면 당연하게 느껴지지만 이는 많은 정리에 사용됩니다.
예시 문제 1)


일단 해당 문제에서 수열을 함수에 대응시켜서 생각하기는 힘든 것 같습니다. 그럼 위와 같은 풀이는 어떨까요? 만약 이렇게 작성한다면 0점을 받을 겁니다... 왜냐하면 수열의 수렴성을 모르기 때문에 a_n = a_n+1 이라고 단정지을 수 없기 때문입니다. 그렇다면 수열의 수렴성은 어떻게 보일 수 있을까요? 바로 단조수열 정리입니다.
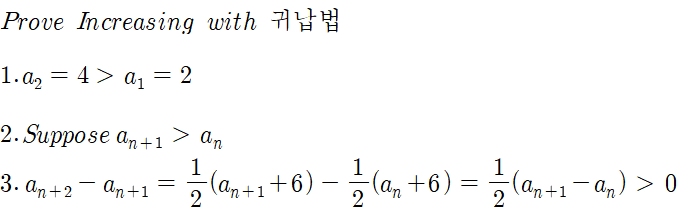

이 때 상한을 6 으로 설정한 이유는 위에서 구한 값을 한번 사용해 봤습니다. 위의 2가지 사실을 증명했으니 해당 수열은 수렴한다는 사실을 알 수 있으며 위의 처음 Wrong Solution을 사용할 수 있음을 보이고 답을 구하면 정답이 되겠습니다~
Series Rule

해당 내용은 Limit Rule과 비슷합니다. 그리고 해당 규칙을 지키지 않아서 생긴 재밌는 사례가 있는데요, 자연수의 모든 합은 -1/12 라는 라자누이의 합.. 유명한 예시인데요, Sn 이 수렴하지 않은데 (iii) 성질을 이용해서 이상한 결과가 나타나게 됩니다.
이번 포스팅은 수열과 함수의 차이점, 그에 따른 주의할 점을 중심으로 다뤄봤고 수열에서 사용되는 유용한 정리를 짧게 설명해봤는데요, 이는 Sequence와 Series 의 기초인 만큼 이번 포스팅은 매우 짧았던 것 같습니다. 다음에는 급수의 수렴 판정법에 대해서 알아보겠습니다.
'대학 공부 > 미적분학I' 카테고리의 다른 글
| [미적분학I] 감점되기 쉬운 요소 (0) | 2024.04.07 |
|---|---|
| [미적분학] 역쌍곡선 함수의 미분 - feat. 역삼각함수 (0) | 2024.03.31 |
| [미적분학I] 역삼각함수 미분 (0) | 2024.03.28 |