가우스 소거법이나 역행렬 혹은 여러 factorization 을 사용하여 Ax = b의 해를 구하고자 노력했습니다. 하지만 일반적으로 해가 존재하지 않는 경우가 훨씬 많습니다. 이러한 경우에 orthogonal 개념을 이용하여 최소 오차를 구하고자 합니다!
1. 정사영 ( 배경 지식 )
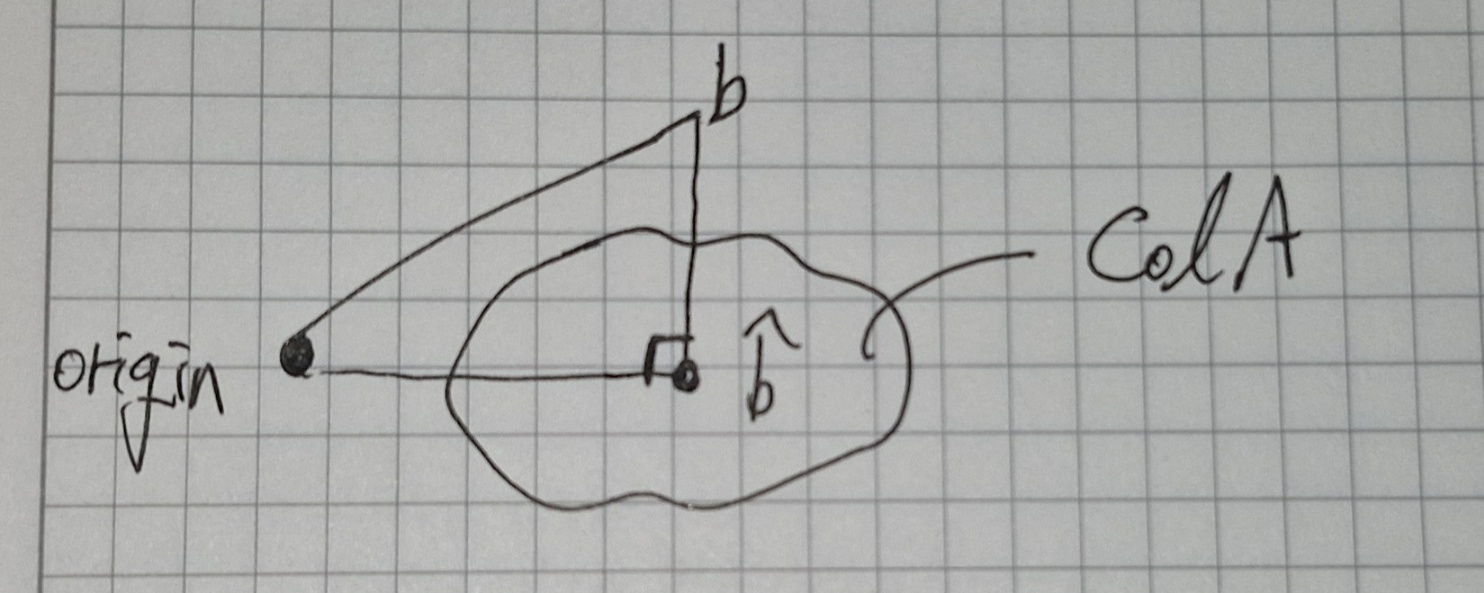
만약 b가 Col A 에 속하지 않다면 해는 존재하지 않습니다. 따라서 b는 아니지만 Col A에 속하는 원소 중, b와 거리가 가장 작은 값을 선택해야 합니다. 해당 포스팅에선 b hat 이라고 명명하겠습니다.
중학교에서 배웠듯이 가장 짧은 거리는 "직선" , "수직" 의 특성을 띈 수선입니다. 그렇다면 b hat은 어떻게 구할 수 있을까요? 해당 내용은 아래 글을 참고해주세요.
[전산수학I] Orthogonal의 기본적인 개념들
해당 개념을 소개하기 앞써 Orthogonal의 중요성은 언급하고자 합니다. Orthogonal은 직교를 뜻하며 일반적인 Basis 를 나중에 소개할 Gram-Schmidt 혹은 QR factorization을 활용해 직교 좌표계를 만든 후, 정사
study-cat.tistory.com
2. 행렬의 곱과 선형 변환
이전의 포스팅에서 행렬끼리의 곱은 합성 함수와 비슷하다고 하였습니다. 그렇다면 (UT)U , U(UT) 같은 행렬은 무엇을 의미할까요?
기본적으로 행렬을 왼쪽 matrix의 행과 오른쪽 matrix 의 열의 원소를 곱한 값의 합을 의미합니다. 그리고 전치행렬이 적용된 경우엔 행 x 열 이 아니라 열 x 열 혹은 행 x 행 꼴로 연산을 바꾼다고 이해할 수 있습니다.
예시로 (UT)U 는 U의 열과 U의 열의 각 원소를 곱한 합을 나타냅니다! 해당 행렬 곱의 의미는 U의 열벡터끼리의 내적 matrix를 만드는 것과 같습니다. 또한 U(UT) 는 위 내용과 이전 포스팅 내용을 합쳐서 생각해보면 projection matrix임을 알 수 있습니다.
※ 주의사항

행렬 곱은 합성함수와 비슷하다고 말했는데,, 주의할 점이 한 가지 존재합니다. 그것은 바로 "치역" 이 달라질 수 있다는 사실인데요, (AT)A = I_m 이면 R_m 을 span 한다고 생각할 수도 있지만 항상 그렇지 않습니다. 왜냐하면 변환하는 과정에서 치역의 차원이 달라지며 중간 행렬의 정의역이 달라지기 때문입니다.
즉 (AT)A 인 경우에 A를 곱할 때 정의역은 Rm 이고 치역은 Rn 의 subspace가 되며 AT 를 곱할 때의 정의역은 Rn의 subspace 즉 A의 치역이 되며 이의 치역이 항상 Rm 을 span 한다고 말할 수 없다는 뜻 입니다.
3. Least-Squre-Method
위에서 소개한 정사영의 개념으로 b hat을 구할 수는 있지만 매우 번거롭기에 다른 방법을 모색해보았습니다.

이 때 행렬 A는 orthogonal 하거나 n by n 이라는 제약을 필요로 하지 않습니다. 해당 식의 원리는 간단한데요, 만약 해가 없다면 저희는 그나마 가장 가까운 점 b hat을 찾을라고 할것이며, b hat의 특성인 b - b hat 은 Col A 와 수직임을 이용할 것입니다.
Col A 와 수직하다는 뜻은 A의 basis 와 내적하면 값이 모두 0 이여야 하는데,,, 구지 basis를 찾을 필요 없이 그냥 A의 모든 column 들과 내적해보고 전부 0 이면 Col A 와 수직하다고 말할 수 있습니다. 따라서 위 방정식을 풀면 x hat을 구할 수 있으며 A * x hat = b hat 을 구할 수 있습니다.
단 b hat 은 unique 하지만 x hat은 not unique 임을 기억해주세요!
이번 포스팅에서는 머신러닝이나 공학에서 굉장히 많이 사용되는 내용에 대해 다뤄보았으며 이를 쫌 더 이해하기 위해 선형변환의 치역의 변화에 대해서도 알아보았습니다. 피드백을 남겨주시면 즉각 반영해보도록 하겠습니다.
다음에는 대각화와 SVD, 그리고 공분산 닮은 행렬에 대해 소개해보겠습니다.
'대학 공부 > 전산수학I' 카테고리의 다른 글
| [전산수학I] Orthogonal의 기본적인 개념들 (0) | 2024.05.27 |
|---|---|
| [전산수학I] 부분 공간(Subspace)와 차원(Dimension/Rank) (0) | 2024.05.16 |
| [전산수학I] 행렬과 행렬의 곱셈 (feat. 기하적 해석) (0) | 2024.04.11 |
| [전산수학I] 풀이과정 팁 & 감점요인 (feat. Theorm) (0) | 2024.04.09 |
| [전산수학I] Linear Transformation(선형변환) (0) | 2024.04.06 |