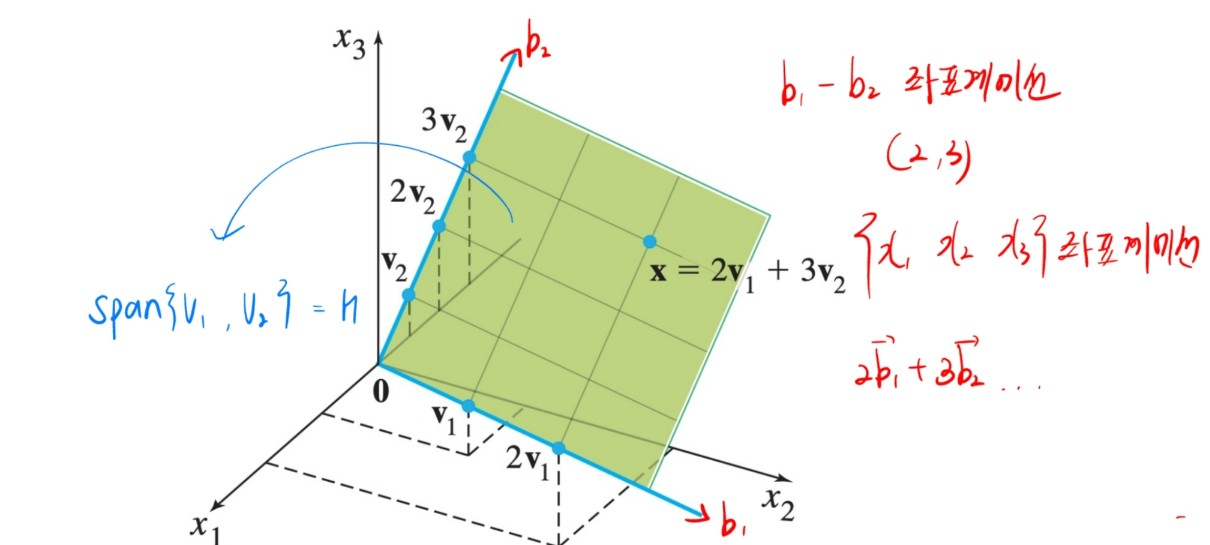
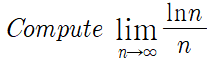해당 포스팅에서 수열과 함수의 대응성과 단조수열정리에 대해 알아볼건데요, 시험에서 감점당하기 좋은.. 부분과 기초적인 부분을 중심으로 알아보겠습니다.  해당 포스팅은 Calculus Early Transcendentals 원서를 기반으로 작성했습니다. 이번 내용은 기초적인 내용이기에 짧습니다.. 1. 수열과 함수의 대응성 기본적으로 수열에서 로피탈은 사용할 수는 없습니다. 왜냐하면 수열은 실수에 대해서 정의된 것이 아닌 정수로 끊겨져 있기 때문입니다. 따라서 수열을 연속인 함수와 대응할 경우에만 로피탈을 사용할 수 있습니다. If lim x->infinity f(x) = L and f(n) = a_n (n = integer), then limit n->infinity a_n = Lf(n) = a_n 으로..

부분공간(Subspace)space, 공간은 벡터들의 집합을 말하는데, 어떤 공간 집합의 부분 집합을 Subspace라고 하며 아래 3가지 규칙을 만족해야 합니다. Let H is Subspace of Rn1. H는 zero vector를 포함해야 한다.2. H에 속하는 임의 벡터 u, v에 대하여 u+v 또한 H 집합에 속해야 한다.3. H에 속하는 임의 벡터 u에 대하여 cu 또한 H 집합에 속해야 한다. 이를 만족하는 Subspace도 크게 2가지로 나눌 수 있습니다. 1. Zero subspace - 오직 zero vector만 포함2. Nonzero subspace - 다른 vector들도 포함만약 Nonzero subspace라면 (2), (3)에 의해 무한한 크기의 집합이 될 것이며 선형적인..